WebGL Setup
From now on, some basic exercises will be implemented using WebGL. To be able to correctly run the exercises, you may have to change some settings in the Firefox configurations. Type about:config into the Firefox bar, hit enter and skip the warning. Search for webgl.disabled and set its value to false. If you encounter an error saying "Cross-Origin Request Blocked" on the console and nothing is loaded, you can either setup a server (e.g. liveServer-extension for visual studio code) or set security.fileuri.strict_origin_policy to false in the Firefox config. It might be required to refresh the index.html page several times after that to apply the changes and make everything work!
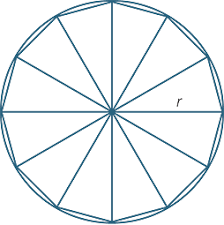
The aim of the first task is to rasterize a circle using triangles.
The result should be similar to the arc() and SVG circles you know from the first exercise sheet.
On the right, you can see a schematic of the circle construction from triangles.
The canvas below only shows a single triangle so far.
Change the code in Basic1.js to build a vertex buffer object and an index buffer object describing a circle
with radius r (currently set to 0.7) around the center point c (currently set to [0.3, 0.2]).
Each vertex should only be stored once - use the Indexed Face Set structure shown in the lecture to keep the vertex buffer small: Do not store points twice but store them once and reference them twice (or more times) using an index buffer.
You can change the number of segments the circle is composed of by changing slices
in order to debug your code.
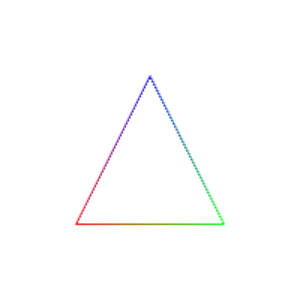
The following task introduces you to different methods for variable passing between host program, vertex shader and fragment shader: vertex attributes and varying variables.
The goal of the task is to reproduce the triangle on the left in the canvas in the middle by coloring the black triangle and only drawing its borders.
A central property of geometry are so-called vertex attributes, which means vertex specific data. The most common and most important vertex attribute is the position, but arbitrary other attributes can be defined.
In this subtask, you should define a color attribute and pass it to the shader program in order to color the triangle. You have to complete several steps to define and use this additional vertex attribute:
-
in
Basic2.js: Define a second attribute (in addition to the position) by extendingvertices. The color should be plain red, plain green and plain blue for the three vertices, as you can see in the image. For the shader stage to know which of the entries inverticesbelong to the position attribute, define the strides and offsets for the position and color attributes using the three functionsgl.getAttribLocation(),gl.enableVertexAttribArray()andgl.vertexAttribPointer(). -
in the vertex shader: Create an attribute whose name you can use for
gl.getAttribLocation(). This attribute will hold the additional color property of each vertex. Create a varying variable and assign the color to it to interpolate the color for each pixel and pass the interpolated value to the fragment shader. - in the fragment shader: Define the varying variable again to enable variable passing from the vertex shader. Use this variable to color each pixel.
The color attribute can also be interpreted as barycentric coordinates: For each pixel inside the triangle, the three color values contain information about its distance to the three points. Use this information to only render the border of the triangle.
Data transfer between CPU and GPU, or between your JavaScript and shader code is a fundamental necessity. Besides the previously introduced vertex attributes, also constant data can be passed from the JavaScript code to the shader using so-called uniform variables. The values passed to the shaders using uniform variables are constant for all vertices / fragments of a draw call.
These variables have to be declared in the respective shader[s] by declaring a global variable as uniform.
In order to pass data to the shader, you have to retrieve its location using gl.getUniformLocation().
Using this location data can then be assigned using gl.uniform*().
In this task we render a circle using a fragment shader.
Instead of a lot of triangles we render a single screen-space aligned quad.
The quad is rasterized and can be shaded using the shader shader_circlefromquad.fs.
Currently, we shade everything orange.
We want you to render a smooth circle by removing all pixels that are outside the circle radius r using discard.
Your task is to draw a orange circle around the center of the quad with the radius r = 0.8. Additionally, use a smoothing margin for anti-aliasing with a width smoothMargin = 0.01. Implement the following subtasks:
-
Create a uniform variable
vec2 canvasSizeand retrieve its location in your JavaScript application. Note: If you do not use the variable in your shader it might be possible that you cannot retrieve its location. Pass the canvas size to the shader uniform usinggl.uniform2f(). -
Map the fragment's coordinate
gl_FragCoord.xyinto the range [-1,1]2. Hint: You can debug usinggl_FragColor = vec4(abs(uv), 0.0, 1.0);. -
Discard all fragments outside the radius
r; color all fragments inside with orange. -
Interpolate the opacity (
gl_FragColor.a) for all fragments inside[r - smoothMargin, r]. You can use the GLSL functionclamp().

In this task we want you to implement some basic linear transformations (i.e. transformations with $\vec{t} = 0$): rotation, scaling and shearing.
The corresponding functions can be found in Basic4_1.
Implement them to rotate, scale and shear the input triangle by the given values.
The result should look like the row above.
A rotation transformation can be substituted by a series of shear transformations:
\begin{eqnarray}
\nonumber
\left(
\begin{array}{*{3}{c}}
\cos(\alpha) & -\sin(\alpha) \\
\sin(\alpha) & \cos(\alpha) \\
\end{array}
\right)
=
\left(
\begin{array}{*{3}{c}}
1 & -\tan(\frac{\alpha}{2}) \\
0 & 1 \\
\end{array}
\right)
\left(
\begin{array}{*{3}{c}}
1 & 0 \\
\sin(\alpha) & 1 \\
\end{array}
\right)
\left(
\begin{array}{*{3}{c}}
1 & -\tan(\frac{\alpha}{2}) \\
0 & 1 \\
\end{array}
\right)
\end{eqnarray}
Implement the shearing functions to perform a rotation and call them with the right parameters in Basic4_2.
Render the triangle after each shearing step.
After the third shearing step, the triangle should look like the rotated triangle from the previous subtask.
Given two affine transformations $f_1$ and $f_2$
with linear parts $\mathbf{A}_1$,
$\mathbf{A}_2$ and translation vectors $\vec{t}_1$, $\vec{t}_2$ respectively, the composition $f_2 \circ f_1$ is also affine:
$$f_1(\vec{x}) = A_1\vec{x} + \vec{t}_1 \text{ and } f_2(\vec{x}) = A_2\vec{x} +\vec{t}_2 \Rightarrow (f_2 \circ f_1)(\vec{x}) = A_{1,2}\vec{x} + \vec{t}_{1,2}$$
Determine its linear part $A_{1,2}$ and its translation vector $\vec{t}_{1,2}$.
Implement the corresponding formula in the function Basic4_3.CompositeAffineTransformations().
Below you see from left to right the input triangle, the triangle transformed with $f_1$, the triangle transformed with $f_1$ and $f_2$ in succession and the input triangle transformed with the composition of both transformations.
Note that the two rightmost triangle images should be the same.